二叉排序树

234 树

一、引入

​ 在二叉树中，每个节点有一个数据项，最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点，就是多叉树（multiway tree）。
​ 2-3-4树，就是多叉树，它的每个节点最多有四个子节点和三个数据项。首先，2-3-4树像红黑树一样是平衡树。它的效率比红黑树稍差，但是编程容易。

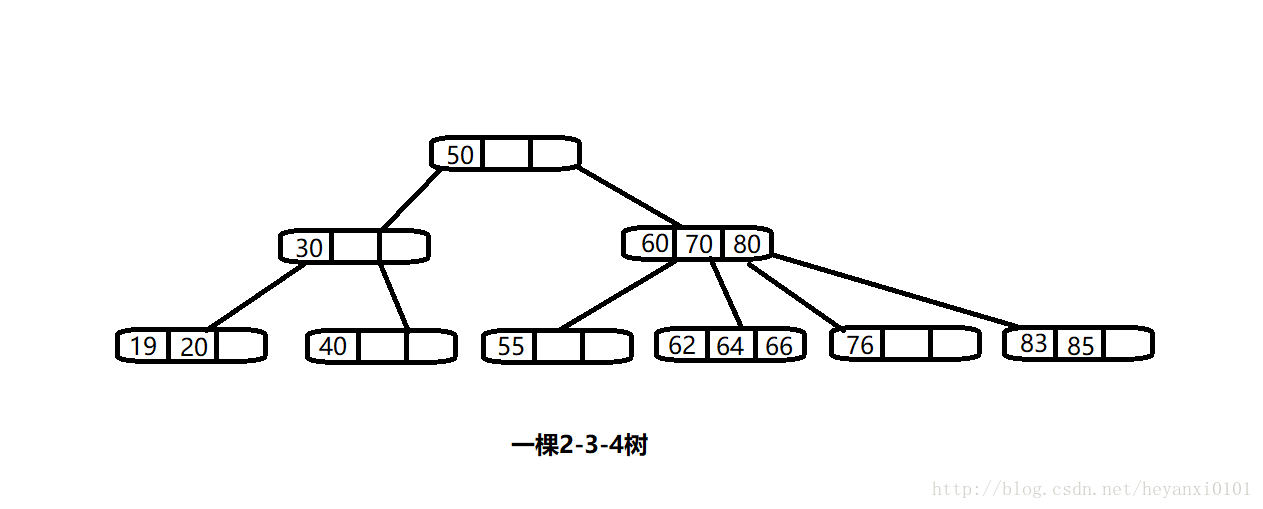
· 上图展示的就是一棵2-3-4树，每个节点可以保存一个、两个或者三个数据项。
· 上图中上面三个节点有子节点，底层的六个节点都是叶节点，没有子节点。2-3-4树中所有的叶节点都是在一层上的。

二、2-3-4树名字的含义与特性

2-3-4树中的2、3、4的含义指的是一个节点可能含有的子节点数。对非子叶节点有三种可能的情况：

​ · 有一个数据项的节点总是有两个子节点
​ · 有两个数据项的节点总是有三个子节点
​ · 有三个数据项的节点重是有四个子节点

上述的重要的关系决定了2-3-4树的结构，比较而言，叶节点没有子节点，然而他可能还有一个、两个、三个数据项。空节点是不会存在的。在2-3-4树中不允许只有一个连接。有一个数据项的节点必须总是保持两个连接，除非它是叶节点，在那种情况下没有连接。

234树主要有以下特点：

• 一个节点最多可以存储3个数据项。

• 一个节点（非叶节点）最多拥有4个子节点。

• 数据项个数与子节点数量关系为：子节点数量 = 数据项个数 + 1。

  • 一个节点（非叶节点）存有1个数据项时，拥有2个子节点。

  • 一个节点（非叶节点）存有2个数据项时，拥有3个子节点。

  • 一个节点（非叶节点）存有3个数据项时，拥有4个子节点。

• 234树中不存在空节点（没有数据项的节点），这个可以从后面的分裂看出来。

三、数据插入规则

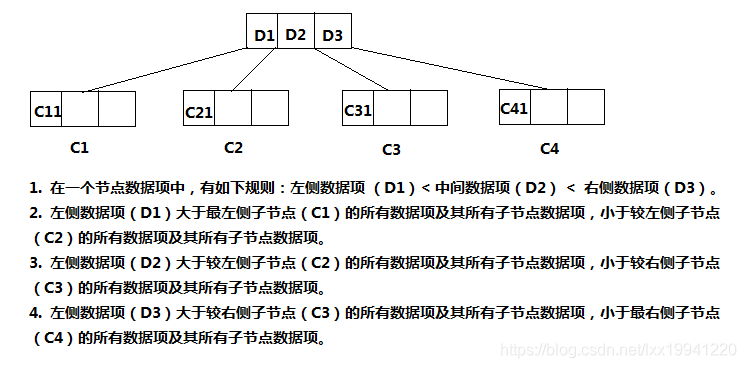
假如一个节点中有三个数据项（从左往右为：D1，D2，D3），那么其4个子节点（从左往右为：C1，C2，C3，C4），有如下大小关系：C1节点数据项及其子节点数据项 < D1 < C2节点数据项及其子节点数据项 < D2 < C3节点数据项及其子节点数据项 < D3 < C4节点数据项及其子节点数据项 。

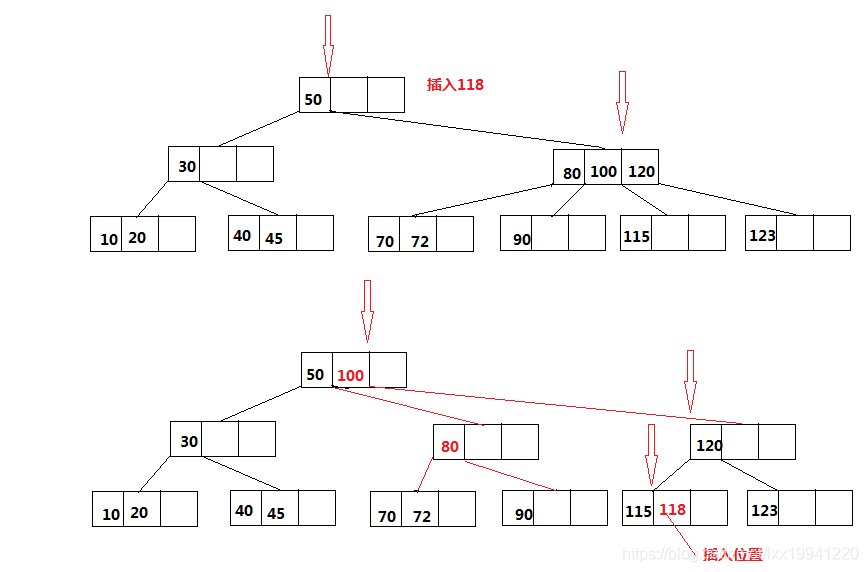
四、插入数据

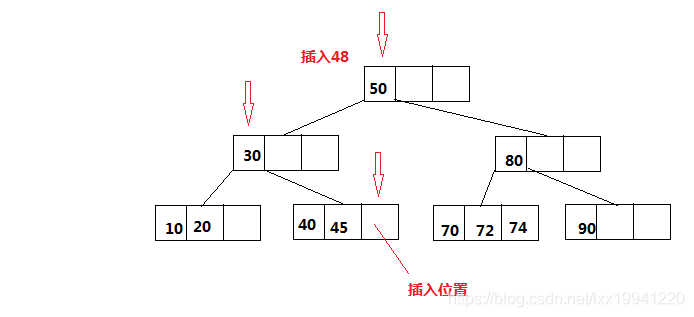
234树插入数据，数据总是插入在叶子节点，跟二叉树一样会向下查找合适的叶子节点，再此过程中核能会发生一系列节点变换（节点分裂），找到叶子节点后，然后根据节点数据项排列顺序（左侧数据项 < 中间数据项 < 右侧数据项）将数据放入节点数据项中。

五、节点分裂

插入数据时，在向下寻找过程中如果遇到了数据项已经满了的节点（拥有三个数据项），将会对改节点进行分裂，假如节点三个数据项从左往右为D1、D2、D3，四个子节点从左往右分别为C1、C2、C3、C4，分裂规则是：

将D2数据项上移，作为父节点的数据项（父节点最多只有两个数据项），创建分裂节点的兄弟节点，将D1数据项作为兄弟节点的数据项，C1，C2作为兄弟节点的子节点，分裂完毕。
如果D2节点上移过程中，没有父节点，即分裂节点为根节点，则新建根节点，然后D2作为根节点的数据项。