排序(三)归并排序 1 描述 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并 。归并排序是一种稳定的排序方法。– 百度百科
2 步骤
将数组分成两个部分,一般是取中值分成大小相差不大于1的两个数组
左右两边数组继续执行步骤一,直至数组长度变为1 (递归)结束条件是数组大小为1
将左右两边排过序的数组进行合并(数组里只有一个数自然就是有序的了)
3 图示过程 引用自 : https://www.jianshu.com/p/33cffa1ce613
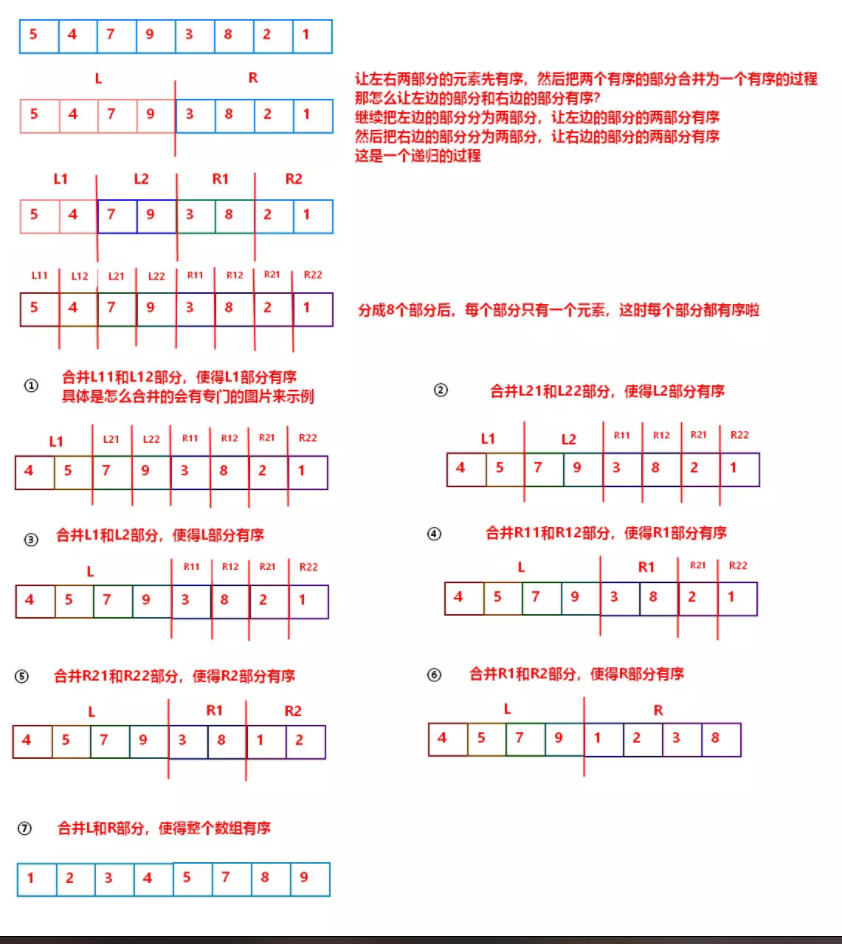
3.1 流程
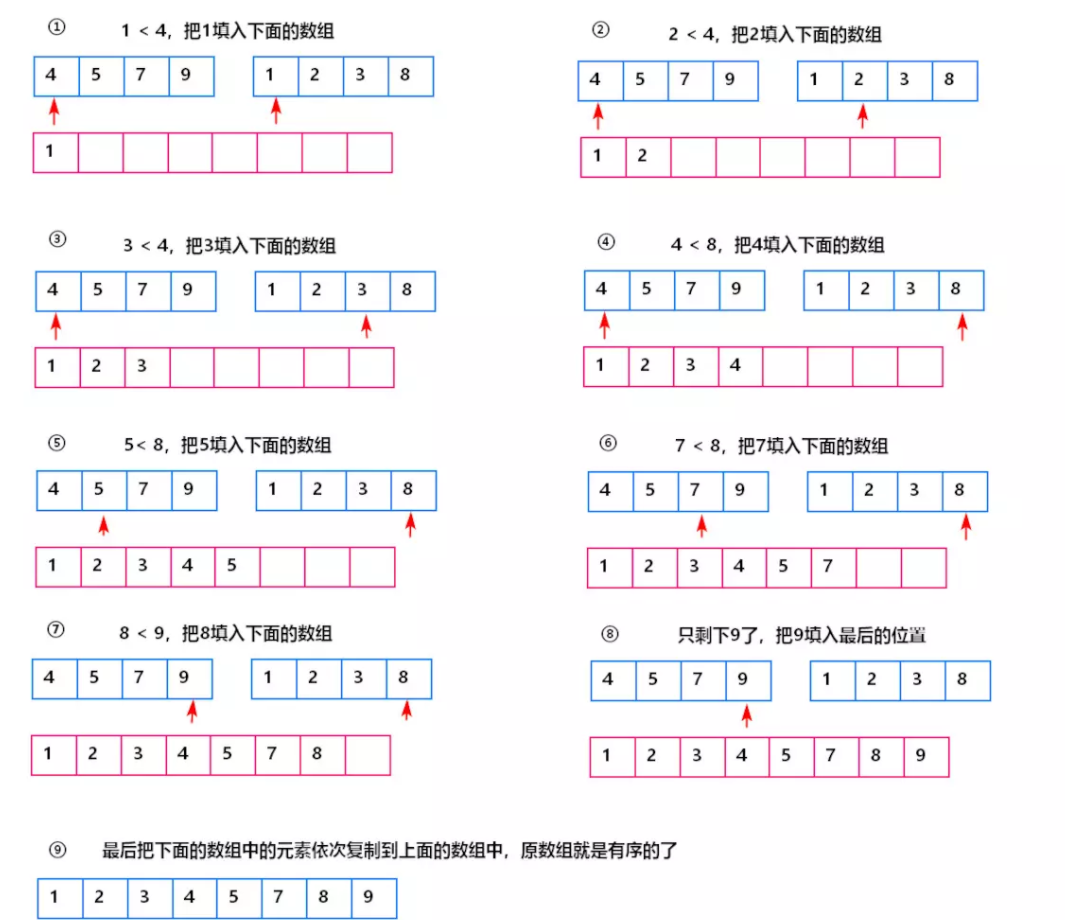
3.2 合并两个有序数据的流程
4 复杂度
时间复杂度:O(nlogn) **空间复杂度:O(N)**,归并排序需要一个与原数组相同长度的数组做辅助来排序
稳定性:归并排序是稳定的排序算法
5 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public void mergerSort (int [] a) { int [] left = new int [a.length /2 ] ; int [] right = new int [a.length - left.length]; System.arraycopy(a,0 ,left,0 ,left.length); System.arraycopy(a,left.length,right,0 ,right.length); if (left.length!=1 ){ mergerSort(left); } if (right.length != 1 ){ mergerSort(right); } int i = 0 , j =0 , k = 0 ; for (;k<a.length;k++){ if ( i >= left.length ){ a[k] = right[j] ; j++; }else if ( j >= right.length ){ a[k] = left[i] ; i++; }else if (left[i] < right[j]){ a[k] = left[i] ; i++; }else { a[k] = right[j] ; j++; } } }
下面是 https://www.jianshu.com/p/33cffa1ce613 博客的代码实现 ,我一开始以为他的代码会比我上面的要快一些 ,因为我每次都新开了两个数组空间 ,但是实际上并没有 (可能是我没有新开结果的数组)。 在处理随机的150000 条数据中他会慢上2 - 3毫秒 , 极少数情况他会比我的实现快。不过他的代码写的确实比我强,你们看看就知道了。
tips: 经过对System.arraycopy()一些测试发现他在数据量大(10000 是个分界点)的情况下是比 普通循环赋值是要快很多的 ,但是 在10000 以下 是比普通的循环复制慢很多
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public void mergerSort (int [] a , int le ,int r) { int mid = (le + r) >> 1 ; if (r!=le){ mergerSort(a , le , mid); mergerSort(a , mid + 1 , r); } int [] temp = new int [r-le+1 ]; int i = le , j = mid + 1 , k = 0 ; while (i <= mid && j <= r){ temp[k++] = a[i] <= a[j] ? a[i++] : a[j++]; } while (i <= mid){ temp[k++] = a[i++]; } while (j <= r){ temp[k++] = a[j++]; } for (int o = 0 ; o < temp.length; o++) { a[le+o] = temp[0 ]; } }